Bigarren mailako funtzio polinomikoa edo funtzio koadratikoa grafikoki adieraztean guztiontzako ezaguna den parabola deritzon konika lortzen da.
Derrigorrezko bigarren hezkuntzan oinarrizko funtzioen gaian funtzio koadratikoa aztertzen dute gure ikasleek, eta funtzio honen adierazpen grafikoa zuzen marrazteak duen garrantzia azpimarratzen ohi dugu irakasleok. Honela, hainbat ezaugarri: ahurra-ganbila, ebaki puntuak OY eta OX ardatzekiko, simetria ardatza, erpina eta balio taula kalkulatu ondoren, parabola grafikoki adierazten dute.
Ezaugarri guzti hauen artean berebiziko garrantzia ematen zaio parabolaren simetria ardatza eta erpina ematen duen formulari: x = -b/2a, eta formula hau, inolako justifikaziorik izan gabe, buruz ikasten dute ikasleek.
Baina, hain beharrezko da formula hori? Badago parabola bat marrazterik aipatutako formula buruz jakin gabe? Edo, bestela, justifika dezakegu zergatik x=-b/2a? Izan dezakegu funtzioaren koefizienteak ikusi bezain pronto parabolaren eskema mentala? Nola?
Bi puntu simetriko baino ez dugu behar. Baina, ze bi puntu dira egokienak? OX ardatzarekiko ebaki-puntuak? Eta ez badu OX ardatza ebakitzen? Nola kalkula ditzakegu bi puntu simetriko era erraz batean eta buruz?
Parabolaren berehalako bi puntu simetriko:
Parabola y=c zuzen horizontalarekin mozten badugu, OY ardatzarekiko ebaki puntu bat (0,c) eta bere simetrikoa (-b/a,c) izango ditugu. Bi puntu hauen abszisen batura erdiak erpinaren abszisa emango digu: x=-b/2a. Honela parabolaren irudi mentala izango dugu (a koefizientea positiboa bada ahurra eta negatiboa balitz ganbila).
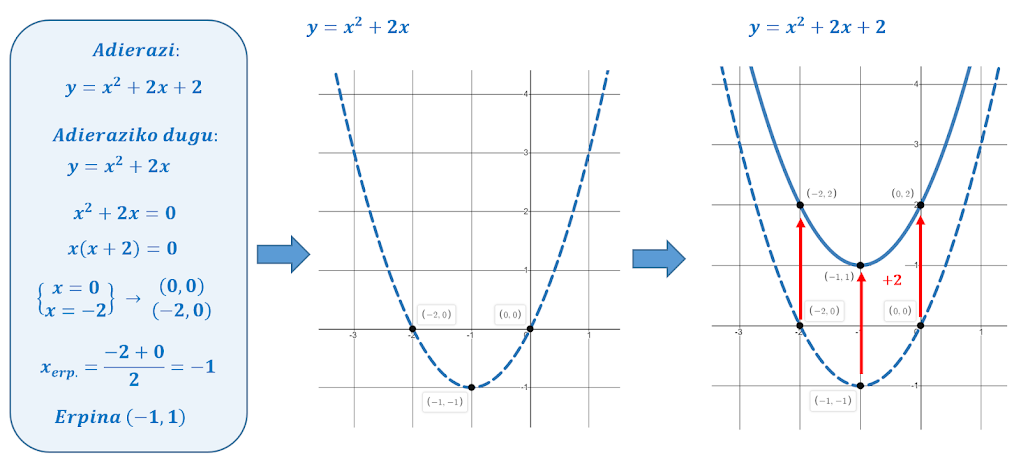
Funtsean goiko adibideetan erabilitako teknika, beste honekin identifika daiteke: c=0 duen parabolaren adierazpena egin ondoren, lorturiko parabola c parametroak adierazitako distantzia desplazatu bertikalki. Adibidez:
ADIBIDE 3
Konturatu parabola ebakitzen duen edozein funtzio konstante y=k erabil daitekeela bi puntu simetriko aurkitzeko. Zuzen horizontal horrek parabola puntu bakar batean ebakitzen badu; hau da, ukitzailea bada, orduan naitaez ukitze-puntu horretan erpina (maximoa edo minimoa) aurkituko da. Argi dago, azkar eta buruz adierazpen grafikoa lortzeko zuzen egokiena y=c dela, adibideetan ikusi dugun bezala.
Deribatuaren irizpidea:
Aurrerago, batxilergoan, deribatua erabil dezakegu parabolaren muturra kalkulatzeko, beharrezko baldintza aplikatuz; hau da, deribatua berdin zero eginez. Honela, berriz ere, erpinaren abszisa lortzen da x=-b/2a. Ondoren, bi puntu simetriko kalkulatzen dira funtzioa ebaluatuz (-b/2a)+n eta (-b/2a)-n balioetan. Puntu gehiago behar izanez gero, n-ri balio desberdinak emango dizkiogu.
a, b eta c koefizienteen esanahia:
a parametroaren zeinuak kurbadurari buruzko informazioa ematen digu (a>0 bada ahurra eta a<0 bada ganbila). Balio absolutuz, a koefizienteak parabolaren irekiera determinatuko du: a-ren balioa txkitzean parabola zabaldu egiten da, bigarren mailako terminoaren balioren txikitzea dakarrelako; ondorioz, a>0 den kasuan y ordenaturen balioa beherago izango dugu. b parametroarekin konbinatuz, erpinaren abszisaren kokapenean ere parte hartzen du a koefizienteak: x=-b/2a.
a eta b koefizienteak konstate mantenduz, c parametroak bertikalki gora eta behera eramaten du parabola.
a eta c konstante uzten badira, b koefizienteari balio desberdinak ematen bazaizkio, parabolaren erpina a eta c balioen menpe soilik dagoen beste parabola baten gainean mugitzen da. Ikus dezagun baieztapen honen egiaztapena:
Aukeratu a eta c parametroak, eta eman balio desberdinak b koefizienteari irristatzailea erabiliz. Klikatu karratuan erpinak deskribatzen duen parabolaren ekuazioa ikusteko: